算法笔记（三）——图论（Python实现）

图论

树的存储

邻接矩阵

# 创建一个二维列表表示邻接矩阵
n = 10  # 顶点数量
g = [[0] * n for _ in range(n)]

# 添加一条边a->b
def add_edge(a, b):
    g[a][b] = 1

# 初始化
g = [[0] * n for _ in range(n)]

邻接表

# 创建一个列表表示邻接表
n = 10  # 顶点数量
h = [-1] * n
e = [0] * n
ne = [0] * n
idx = 0

# 添加一条边a->b
def add_edge(a, b):
    global idx
    e[idx] = b
    ne[idx] = h[a]
    h[a] = idx
    idx += 1

# 初始化
idx = 0
h = [-1] * n

树和图的存储

# 邻接表表示的图
N = 100010  # 根据具体需求设置合适的最大节点数量

# 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
h = [-1] * N
# 存储边的目标节点
e = [0] * N
# 存储下一条边的索引
ne = [0] * N
# 边的索引
idx = 0

# 添加一条边a->b
def add(a, b):
    global idx
    e[idx] = b
    ne[idx] = h[a]
    h[a] = idx
    idx += 1

# 初始化
idx = 0
for i in range(N):
    h[i] = -1

树和图的遍历

DFS

def dfs(u):
    st[u] = True
    i = h[u]
    while i!=-1:
        j = e[i]
        if not st[j]:
            dfs(j)
        i = ne[i]

BFS

from collections import deque
q = deque()
st[1] = True
q.append(1)
while q:
    t = q.popleft()
    i = h[t]
    while i!=-1:
        j=e[i]
        if not st[j]:
            st[j] = True
            q.append(j)
        i=ne[i]

拓扑排序

from sys import stdin
from collections import deque

input = lambda:stdin.readline().strip()

def topsort():
    q = deque()
    res = []
    for i in range(1, n+1):
        if ind[i]==0:
            res.append(i)
            q.append(i)
    
    while q:
        u = q.popleft()
        for v in g[u]:
            ind[v] -= 1
            if ind[v]==0:
                q.append(v)
                res.append(v)
    
    return res
    
n = int(input())
ind = [0]*(n+1)
g = [[] for _ in range(n+1)]

for i in range(1, n+1):
    a = list(map(int, input().split()))
    for j in range(len(a)-1):
        g[i].append(a[j])
        ind[a[j]]+=1
    
res = topsort()
print(*res, sep=' ')

奖金

from sys import stdin
from collections import deque

def topsort():
    res = []
    q = deque()
    ans = 0
    for i in range(1, n+1):
        if ind[i]==0:
            res.append(i)
            q.append((i, 100))
            ans += 100
    while q:
        u, m = q.popleft()
        for v in g[u]:
            ind[v] -= 1
            if ind[v]==0:
                q.append((v, m+1))
                res.append(v)
                ans += m+1
                
    if len(res)==n:
        print(ans)
    else:
        print("Poor Xed")


n, m = map(int, input().split())

ind = [0]*(n+1)
g = [[] for _ in range(n+1)]

for i in range(m):
    a, b = map(int, input().split())
    ind[a] += 1
    g[b].append(a)
    
topsort()

LCA

def lca(x,y):
    if dep[x] < dep[y]:
        x,y = y,x
    d = dep[x]-dep[y]
    while d:  # 循环直到深度差为 0
        v = d & -d  # 获取 d 的最低位的 1 所在的位置
        i = v.bit_length() - 1  # 计算最低位的位置索引
        x = fa[i][x]  # 将节点 x 上移到和节点 y 同一深度
        d -= v  # 更新深度差
    if x==y:
        return x
    for k in range(K-1, -1, -1):
        if fa[k][x] != fa[k][y]:
            x = fa[k][x]
            y = fa[k][y]
    return fa[0][x]

# 初始化深度以及父节点信息
dep[x]=dep[val]+1
dep[y]=dep[val]+1
fa[0][x] = val
fa[0][y] = val

for k in range(K-1):
    fa[k+1][x] = fa[k][fa[k][x]] # 自己的第2^(1+1)级父亲即为 自己的第2^(1)级父亲 的第2^(1)级父亲
    fa[k+1][y] = fa[k][fa[k][y]]

祖孙询问

from sys import stdin
from collections import deque, defaultdict
from math import inf

K = 17
N = int(4*10e4) + 10
dep = [inf]*(N)
fa = [[0]*N for _ in range(K)]


def bfs():
    dep[0] = 0; dep[root] = 1
    q = deque([root])
    while q:
        u = q.popleft()
        for v in g[u]:
            if dep[v] > dep[u] + 1:
                dep[v] = dep[u] + 1
                q.append(v)
                fa[0][v] = u
                for k in range(1, K-1):
                    fa[k][v] = fa[k-1][fa[k-1][v]]

def lca(x, y):
    if dep[x] < dep[y]:
        x, y = y, x
    d = dep[x] - dep[y]

    while d:
        v = d & -d
        i = v.bit_length() - 1
        x = fa[i][x]
        d -= v

    if x==y:
        return x
        
    for k in range(K-1, -1, -1):
        if fa[k][x] != fa[k][y]:
            x = fa[k][x]
            y = fa[k][y]
            
    return fa[0][x]

n = int(input())
g = defaultdict(list)

for i in range(n):
    a, b = map(int, input().split())
    if b==-1:
        root = a
    else:
        g[a].append(b)
        g[b].append(a)


bfs()
# print(dep)
m = int(input())

for i in range(m):
    x, y = map(int, input().split())
    
    res = lca(x, y)
    if res == x and res != y:
        print(1)
    elif res == y and res != x:
        print(2)
    else:
        print(0)

最短路

单元最短路
- 所有边权为正：
  - 朴素版Dijkstra $O(n^2)$,堆优化版的Dijkstra $O(mlogn)$,
- 存在负权边
  - Bellman-Ford $O(nm)$, SPFA 队列优化的Bellman-Ford, 一般情况：$O(m)$ 最坏情况：$O(nm)$
多元汇最短路：
- Floyed $O(n^3)$

朴素Dijkstra

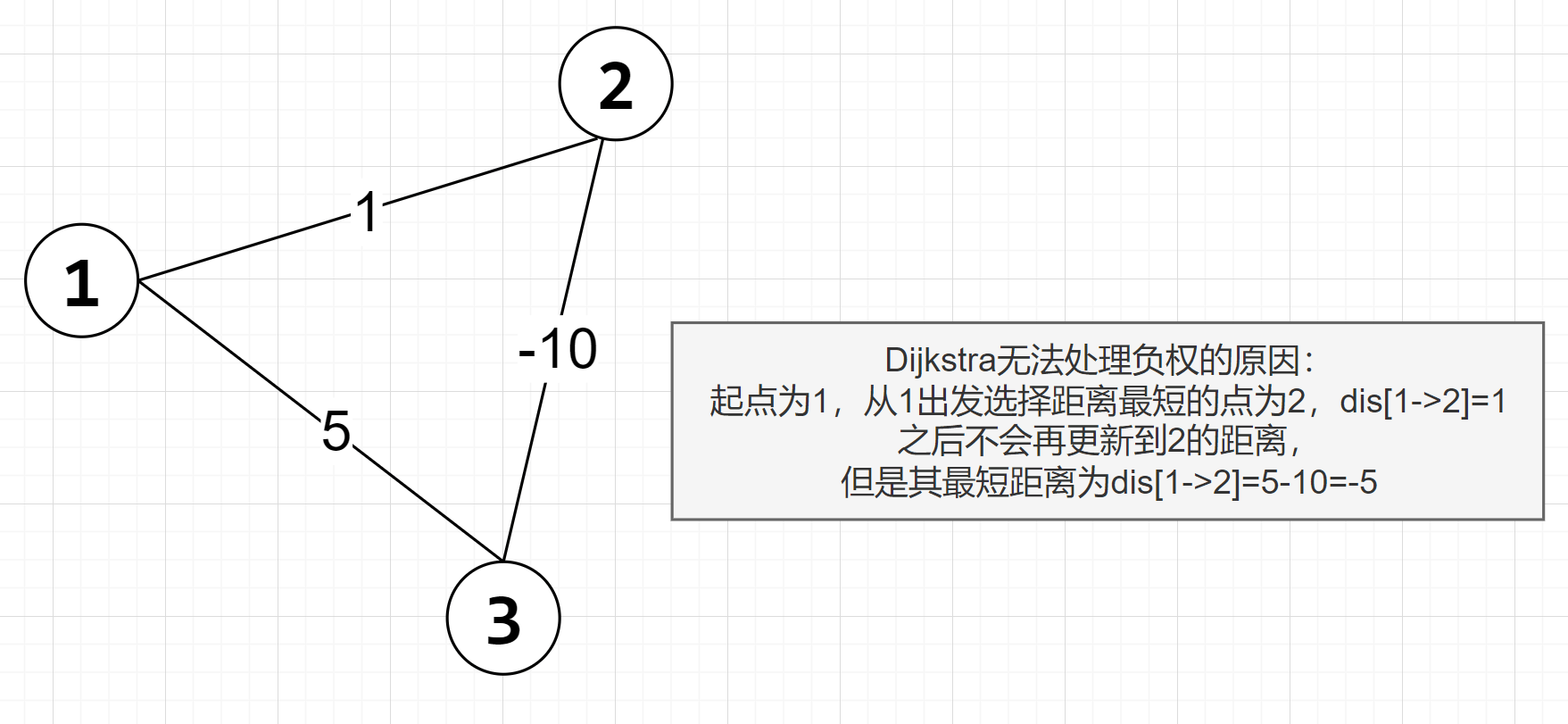
Dijkstra不能处理负权边：

N = int(5e2)+10
INF = 0x3f3f3f3f
g = [[INF]*N for _ in range(N)]
#g = defaultdict(lambda:defaultdict(lambda:INF)) 同样的效果
dis = [INF]*N
st = [False]*N

def dijkstra():
    dis[1]=0
    for i in range(n-1):
        t=-1
        for j in range(1,n+1):
            if not st[j] and (t==-1 or dis[j]<dis[t]):
                t=j
        for j in range(1,n+1):
            dis[j]=min(dis[j], dis[t] + g[t][j])
        st[t]=True
    if dis[n]==INF:
        return -1
    return dis[n]

n, m = map(int, input().split())
for _ in range(m):
    x, y, z = map(int ,input().split())
    g[x][y] = min(g[x][y], z)
    
print(dijkstra())

堆优化版Dijkstra

from heapq import *
import sys
input = lambda:sys.stdin.readline().strip()
N = 150010
INF = 0x3f3f3f3f
e, ne, head, w, dis= [0]*N, [0]*N, [-1]*N, [0]*N, [INF]*N
st = [False]*N
idx=0

def add(a, b, x):
    global idx
    e[idx]=b
    w[idx]=x
    ne[idx]=head[a]
    head[a]=idx
    idx+=1
    
def dijkstra():
    dis[1]=0
    h=[]
    heappush(h, (0,1))
    while h:
        dist, ver = heappop(h)
        if st[ver]: continue
        st[ver]=True
        i=head[ver]
        while i!=-1:
            j=e[i]
            if not st[j] and dis[j]>dist+w[i]:
                dis[j]=dist+w[i]
                heappush(h, (dis[j], j))
            i=ne[i]
    if dis[n]==INF:
        print(-1)
    else:
        print(dis[n])

n, m = map(int, input().split())
for _ in range(m):
    x, y, z = map(int, input().split())
    add(x,y,z)
    
dijkstra()

另一种写法

from sys import stdin
from math import inf
from collections import deque, defaultdict
from heapq import heappush, heappop
input = lambda:stdin.readline().strip()

def dijkstra():
    h = [(0, 1)]
    dis[1] = 0
    
    while h:
        dist, ver = heappop(h)
        if vis[ver]:
            continue
        vis[ver] = True
        for nx, z in g[ver]:
            if dis[nx] > dis[ver] + z:
                dis[nx] = dis[ver] + z
                heappush(h, (dis[nx], nx))
                
    return dis[n]
    

n, m = map(int, input().split())
dis = [inf]*(n+1)
vis = [False]*(n+1)
g = defaultdict(list)

for i in range(m):
    x, y, z = map(int, input().split())
    g[x].append((y, z))

res = dijkstra()
print(res if res != inf else -1)

Bellman-Ford

# n表示点数，m表示边数
dist = [float('inf')] * (n + 1)  # dist[x]存储1到x的最短路距离
# 边，a表示出点，b表示入点，w表示边的权重
edges = []

# 求1到n的最短路距离，如果无法从1走到n，则返回-1。
def bellman_ford():
    dist[1] = 0
    # 如果第n次迭代仍然会松弛三角不等式，就说明存在一条长度是n+1的最短路径，由抽屉原理，路径中至少存在两个相同的点，说明图中存在负权回路。
    for i in range(n):
        for j in range(m):
            a, b, w = edges[j]['a'], edges[j]['b'], edges[j]['w']
            if dist[b] > dist[a] + w:
                dist[b] = dist[a] + w
    if dist[n] > float('inf') / 2:
        return -1
    return dist[n]

SPFA

from collections import defaultdict, deque
import sys
input = lambda:sys.stdin.readline().strip()

N, INF = int(1e5+10), 0x3f3f3f3f

dis, st = [INF]*N, [False]*N
g=defaultdict(list)

def spfa():
    q=deque()
    q.append(1)
    st[1]=True
    dis[1]=0
    while q:
        x=q.popleft()
        st[x]=False
        for y, z in g[x]:
            if dis[y]>dis[x]+z:
                dis[y]=dis[x]+z
                if not st[y]:
                    st[y]=True
                    q.append(y)
    if dis[n]==INF:
        print('impossible')
    else:
        print(dis[n])

n, m = map(int, input().split())
for _ in range(m):
    x, y, z = map(int, input().split())
    g[x].append((y, z))
    
spfa()

判断负环

from sys import stdin
from collections import deque, defaultdict
from math import inf

input = lambda:stdin.readline().strip()

def spfa():
    q = deque()
    for i in range(1, n+1):
        q.append(i)
        st[i] = True
    while q:
        x = q.popleft()
        st[x] = False
        for y, z in g[x]:
            if dis[y] > dis[x] + z:
                dis[y] = dis[x] + z
                cnt[y] = cnt[x] + 1
                if cnt[y] >= n:
                    return True
                if not st[y]:
                    q.append(y)
                    st[y] = True
    return False

n, m = map(int, input().split())

g = defaultdict(list)
cnt = [0]*(n+1)
st = [False]*(n+1)
dis = [0]*(n+1)

for i in range(m):
    x, y, z = map(int, input().split())
    g[x].append((y, z))

res = spfa()

print("Yes" if res else "No")

floyd

from sys import stdin
from math import inf

def floyd():
    for k in range(1, n+1):
        for i in range(1, n+1):
            for j in range(1, n+1):
                d[i][j] = min(d[i][j], d[i][k] + d[k][j])

n, m, k = map(int, input().split())
d = [[0 if i==j else inf for i in range(n+1)] for j in range(n+1)]

for i in range(m):
    x, y, z = map(int, input().split())
    d[x][y] = min(d[x][y], z)
    
floyd()
    
for i in range(k):
    x, y = map(int, input().split())
    print(d[x][y] if d[x][y]!=inf else "impossible")

Prim

from math import inf
from sys import stdin

def prim():
    res = 0
    dis[1] = 0
    for i in range(n):
        t = -1
        for j in range(1, n+1):
            if not st[j] and (t==-1 or dis[t] > dis[j]):
                t = j
        if i and dis[t]==inf:
            return inf
        if i:
            res += dis[t]
        st[t] = True

        for j in range(1, n+1):
            dis[j] = min(dis[j], g[t][j])
    return res
    

n, m = map(int, input().split())
g = [[inf]*(n+1) for _ in range(n+1)]
dis = [inf]*(n+1)
st = [False]*(n+1)

for i in range(m):
    u, v, w = map(int, input().split())
    g[u][v] = g[v][u] = min(w, g[u][v])

res = prim()
if res==inf:
    print("impossible")
else:
    print(res)

Kruskal

import sys
input = lambda:sys.stdin.readline().strip()

def find(x):
    while p[x] != x:
        p[x] = p[p[x]]
        x = p[x]
    return x

def kruskal():
    res, cnt = 0, 0
    ans = []
    for u, v, w in g:
        fu, fv = find(u), find(v)
        if fu != fv:
            res += w
            cnt += 1
            p[fu] = fv
            ans.append((u, v, w))
    
    ans.sort()
    if cnt == n-1:
        print(res)
        # print(ans) # 记录选择的是哪些边
    else:
        print("impossible")
    
n, m = map(int, input().split())
g = []
p = [i for i in range(n+1)]
for i in range(m):
    u, v, w = map(int, input().split())
    g.append((u, v, w))

g.sort(key = lambda e:e[2])

kruskal()

染色法

使用了深度优先搜索算法（DFS）来判断一个图是否是二分图

二分图：顶点分为两个集合，边仅存在于两个不同的集合中，而集合内部都没有边。

Python优先使用BFS，因为DFS会出现各种问题，爆栈，段错误（还没搞清楚原因）等

这段代码使用了染色法来判断一个无向图是否为二分图。下面我来解释一下：

题目大意： 给定一个无向图，判断是否可以将其顶点集合划分为两个不相交的子集，使得每条边的两个端点分别属于这两个子集。如果可以，则输出"Yes"，否则输出"No"。

实现思路：

使用邻接表 g 来表示无向图，其中 g[u] 存储与顶点 u 相连的所有顶点。
定义一个数组 color 来标记每个顶点的染色情况，初始值设为 -1 表示未染色。
定义一个 BFS 函数 bfs(u, c)，其中 u 表示起始顶点，c 表示初始颜色。该函数使用 BFS 遍历图，并将顶点染色，保证相邻顶点颜色不同。
在主体部分，遍历所有顶点，对于每个未染色的顶点，调用 bfs 函数进行染色。如果染色过程中发现相邻顶点颜色相同，则返回 “No”，表示无法划分为二分图；否则返回 “Yes”。

import sys
from collections import deque, defaultdict
input = lambda:sys.stdin.readline().strip()
N = int(1e5)+10
g = defaultdict(list)
color = [-1]*N

def bfs(u, c):
    color[u] = c
    q = deque()
    q.append((u, c))
    while q:
        cur, col = q.popleft()
        for nx in g[cur]:
            if color[nx]==-1:
                color[nx] = 1-col
                q.append((nx, 1-col))
            elif color[nx]==col:
                return False
    return True


n, m = map(int, input().split())
for i in range(m):
    u, v = map(int, input().split())
    # if u==v: #***自环不能去掉***
    #     continue
    if u not in g[v]:
        g[v].append(u)
    if v not in g[u]:
        g[u].append(v)
    
for i in range(1, n+1):
    if color[i]==-1:
        if not bfs(i, 0):
            print("No")
            exit()
print("Yes")

匈牙利算法

题目大意： 给定一个二分图，其中左侧顶点集合为 (N_1)，右侧顶点集合为 (N_2)，图中存在一些边。需要找到尽可能多的匹配，使得左侧的每个顶点最多与一个右侧的顶点相连，而右侧的每个顶点最多与一个左侧的顶点相连。

实现思路：

使用一个二维数组 g 存储图的邻接表表示。其中 g[u] 表示与左侧顶点 u 相连的所有右侧顶点的集合。
定义一个函数 find(x)，用于从左侧顶点 x 开始尝试寻找增广路径，如果找到了增广路径就返回 True，否则返回 False。
在主体部分，遍历左侧的每个顶点，对每个顶点调用 find 函数进行匹配，若成功匹配，则匹配数加一。

from sys import stdin
from collections import defaultdict

def find(u):
    for v in g[u]:
        if not st[v]:
            st[v] = True
            if mat[v]==0 or find(mat[v]):
                mat[v] = u
                return True
    return False
            

n1, n2, m = map(int, input().split())
mat = [0]*(n2 + 1)
g = defaultdict(list)

for i in range(m):
    u, v = map(int, input().split())
    g[u].append(v)
    
    
res = 0
for i in range(1, n1+1):
    st = [False]*(n2 + 1)
    if find(i):
        res += 1
print(res)

DFS之连通性

题意：在一个给定迷宫中，从起点A到终点B是否存在一条路径的问题。迷宫由一个由 '.' 和 '#' 构成的矩阵表示，其中 '.' 表示可通行的格点，'#' 表示不可通行的格点。Extense只能向东南西北四个方向移动到相邻的可通行格点上，而且要求起点和终点都是可通行的。你需要编写一个程序来确定在给定的迷宫中，是否存在一条从A到B的路径。

import sys
input = lambda:sys.stdin.readline().strip()
sys.setrecursionlimit(150000)

dir = [(-1, 0), (0, 1), (1, 0), (0, -1)]
def dfs(x, y):
    if g[x][y]=='#' or vis[x][y]:
        return False
        
    if (x, y)==end:
        return True
        
    vis[x][y] = True
    
    for i in range(4):
        a, b = x + dir[i][0], y+dir[i][1]
        if 0<=a<n and 0<=b<n:
            if dfs(a, b): return True
            
    return False
    

k = int(input())
N = 110
g = [[] for _ in range(N)]
for _ in range(k):
    n = int(input())
    vis = [[False]*(n+1) for _ in range(n+1)]
    for i in range(n):
        g[i] = list(input())
    
    x1, y1, x2, y2 = map(int, input().split())
    
    end = (x2, y2)
    if dfs(x1, y1):
        print("YES")
    else:
        print("NO")

魔板

题目大意：给定一个 8 个格子的魔板，每个格子有一种颜色，用 1 到 8 的整数表示。有三种基本操作可以改变魔板的状态：A：交换上下两行；B：将最右边的一列插入到最左边；C：魔板中央对的4个数作顺时针旋转。现在给定一个目标状态，求用最少的基本操作完成基本状态到目标状态的转换，并输出基本操作序列。

实现思路：

首先实现三种基本操作 A、B、C 的函数。
使用广度优先搜索（BFS）算法来找到从基本状态到目标状态的最短操作序列。
使用一个队列存储待处理状态，并使用一个字典记录每个状态的前驱状态和执行的操作。
在每一步中，尝试对当前状态进行三种基本操作，得到新的状态，如果新状态未被访问过，则将其加入队列，并记录其前驱状态和操作。
当找到目标状态时，根据前驱状态回溯得到最短操作序列。
输出最短操作序列的长度和具体操作序列。

from collections import deque

def A(t):
    return t[::-1]
def B(t):
    return t[3] + t[:3] + t[5:] + t[4]
def C(t):
    return t[0] + t[6] + t[1] + t[3] + t[4] + t[2] + t[5] + t[7]

pre = dict()
def bfs():
    q = deque()
    q.append(st)
    
    while q:
        t = q.popleft()
        if t==ed:
            break
        
        m = [A(t), B(t), C(t)]
        for i in range(3):
            if m[i] not in pre:
                pre[m[i]] = (chr(65+i), t)
                q.append(m[i])
            

nums = input().split()
ed = ''.join(nums)
st = "12345678"

bfs()
cnt = 0
res = ""
while ed != st:
    cnt+=1
    res = pre[ed][0] + res
    ed = pre[ed][1]
print(cnt)
if cnt:
    print(res)

单词接龙

题目大意：给定一组单词和一个开头的字母，要求找出以这个字母开头的最长的“龙”，每个单词最多被使用两次。在构成龙时，两个单词相连时，它们的重合部分合并为一部分，但重合部分的长度必须大于等于1且小于两个单词的长度。

实现思路：

首先读入输入数据，包括单词数 n、n 个单词以及开头的字母。
构建一个字典 g，用于存储每个单词对应的可连接的单词以及对应的重合部分的长度。
对于每一对单词，比较它们的重合部分，如果符合条件，则将其加入字典 g 中。
使用深度优先搜索（DFS）来搜索以开头字母开头的最长的“龙”。
在搜索过程中，使用一个字典 cnt 来记录每个单词的使用次数，每个单词最多只能被使用两次。
递归搜索每个可连接的单词，并更新最长“龙”的长度。
最终输出最长“龙”的长度。

from collections import defaultdict
n = int(input())
wds = []
for i in range(n):
    wds.append(input())
st = input()

g = {w:[] for w in wds}
for i in range(n):
    for j in range(n):
        for k in range(1, min( len(wds[i]), len(wds[j]) )):
            if wds[i][-k:] == wds[j][:k]:
                g[wds[i]].append((wds[j], k))
     
cnt = defaultdict(int)
def dfs(dra, x):
    global ans
    cnt[x] += 1
    ans = max(ans, len(dra))
    for nx, k in g[x]:
        if cnt[nx] < 2:
            dfs(dra + nx[k:], nx)
    
    cnt[x] -= 1

ans = 0
for w in wds:
    if w[0] == st:
        dfs(w, w)
        
print(ans)

分成互质组

题目大意：给定 n 个正整数，要求将它们分组，使得每组中任意两个数互质。求最少需要分成多少个组。

实现思路：

首先读入输入数据，包括正整数的个数 n 和 n 个正整数。
使用深度优先搜索（DFS）来搜索分组的方法。
构建一个列表 g，用于存储分组情况，每个分组是一个列表，列表中存储分组中的数。
编写 DFS 函数，在函数中递归尝试将当前数放入已有的分组或新建一个分组。
在递归过程中，如果当前数可以和某个分组中的所有数互质，则将当前数加入该分组，并继续递归。
如果当前数无法加入任何分组，则新建一个分组，并继续递归。
当所有数都被分组完毕时，更新最少需要的组数。
最终输出最少需要的组数。

from math import gcd
n = int(input())
a = list(map(int, input().split()))
g = []

def dfs(u, i):
    global ans
    if i==n:
        ans = min(ans, u)
        return 
    
    if u>=ans:
        return 
    
    for j in range(u):
        cnt = sum(1 for k in g[j] if gcd(a[i], k)==1)
        
        if cnt==len(g[j]):
            g[j].append(a[i])
            dfs(u, i+1)
            g[j].pop()
    
    g.append([a[i]])
    dfs(u+1, i+1)
    g.pop()

ans = n
dfs(0, 0)
print(ans)

迭代加深加成序列

题目大意：给定一个整数 n，找出满足以下条件的最小长度的“加成序列”：序列的第一个元素为1，最后一个元素为 n，序列中的元素满足每个元素都可以表示为序列中其他两个元素的和。

实现思路：

定义一个深度优先搜索（DFS）函数 dfs，用于搜索符合条件的加成序列。
在 dfs 函数中，使用一个列表 path 来记录当前搜索的加成序列，初始化 path[0] = 1。
递归地搜索加成序列的下一个元素，使得新的元素是前面元素的两两相加的结果，并满足条件 path[u] <= n，其中 u 表示当前搜索的位置。
如果搜索成功，即找到了符合条件的加成序列，返回 True；否则返回 False。
在主程序中，不断读取输入的 n，并通过调用 dfs 函数来搜索符合条件的加成序列。
输出满足条件的加成序列。

def dfs(u):
    if u==dep:
        return path[u-1]==n
        
    vis = [False]*(n+1)
    
    for i in range(u-1, -1, -1):
        for j in range(i, -1, -1):
            s = path[i] + path[j]
            if s>n or s<=path[u-1] or vis[s]:
                continue
            vis[s] = True
            path[u] = s
            
            if dfs(u+1): return True
    return False



path = [0]*(110)
path[0] = 1

while True:
    n = int(input())
    if not n: break
    
    dep = 1
    while not dfs(1):
        dep += 1
    print(*path[:dep])

双向DFS 送礼物

题目大意：达达帮翰翰送礼物，他一次可以搬动的重量之和不超过 W，一共有 N 个礼物，其中第 i 个礼物的重量是 G[i]。求达达在他的力气范围内一次性能搬动的最大重量。

实现思路：

定义两个深度优先搜索（DFS）函数 dfs1 和 dfs2，用于求解达达一次性能搬动的最大重量。
dfs1 函数用于遍历前一半的礼物，求得所有可能的搬动重量之和，并存储在集合 wgh 中。
dfs2 函数用于遍历后一半的礼物，并通过二分查找在 wgh 中找到合适的搬动重量，求得最大重量。
在主程序中，首先读入输入的 W 和 N，然后读入 N 个礼物的重量，并按照重量从大到小排序。
调用 dfs1 和 dfs2 函数求解最大重量，并输出结果。


def dfs1(u, tot):
    if u>k:
        wgh.add(tot)
        return 
    
    if tot + a[u] <= w:
        dfs1(u+1, tot + a[u])
    
    dfs1(u+1, tot)

def dfs2(u, tot):
    global ans
    if u>=n:
        l, r = 0, cnt-1
        while l<r:
            mid = (l+r+1)>>1
            if wgh[mid] + tot <= w:
                l = mid
            else:
                r = mid - 1
        ans = max(ans, wgh[r] + tot)
        return 
    
    if a[u] + tot <= w:
        dfs2(u+1, a[u] + tot)
    
    dfs2(u+1, tot)


w, n = map(int, input().split())
a = []
for i in range(n):
    a.append(int(input()))
a.sort(reverse = True)


wgh = set()
k = n//2
dfs1(0, 0)
wgh = sorted(list(wgh))
cnt = len(wgh)

ans = -1
dfs2(k+1, 0)

print(ans)

37. 解数独 \166. 数独

题目大意：数独是一种益智游戏，要求填写一个9×9的网格，使得每行、每列、每个3×3的九宫格内数字1∼9均恰好出现一次。

实现思路：该实现采用深度优先搜索（DFS）的方法解决数独问题。首先，通过将每个数字映射到二进制位来进行位运算，以便快速获取已填充数字的状态。然后，利用DFS递归填充数独中的空白格子，优先选择当前空白格子填充数字的选择空间较小的位置。递归的终止条件是所有空白格子都填充完毕。

import sys

N = 9
M = 1 << N
row, col, cell = [0] * N, [0] * N, [[0] * 3 for _ in range(3)]
mp = dict()
ones = [0] * M
for i in range(N):
    mp[1 << i] = i
for i in range(1 << N):
    for j in range(N):
        ones[i] += (i >> j) & 1


def lowbit(x):
    return x & -x


def get(x, y):
    return row[x] & col[y] & cell[x // 3][y // 3]


def draw(x, y, t, flag):
    global st, row, col, cell
    if flag:
        st[x * N + y] = chr(49 + t)
    else:
        st[x * N + y] = "."
    v = 1 << t
    if not flag:
        v = -v
    row[x] -= v
    col[y] -= v
    cell[x // 3][y // 3] -= v


def dfs(cnt):
    global st
    if not cnt:
        return True
    minv = 10
    for i in range(N):
        for j in range(N):
            if st[i * N + j] == ".":
                state = get(i, j)
                if ones[state] < minv:
                    minv = ones[state]
                    x, y = i, j
    i = get(x, y)
    while i:
        t = mp[lowbit(i)]
        draw(x, y, t, True)
        if dfs(cnt - 1):
            return True
        draw(x, y, t, False)
        i -= lowbit(i)
    return False


while True:
    st = sys.stdin.readline().strip()
    if st == "end":
        break
    st = list(st)
    cnt = 0
    for i in range(N):
        row[i] = col[i] = M - 1
    for i in range(3):
        for j in range(3):
            cell[i][j] = M - 1

    for i in range(N):
        for j in range(N):
            if st[i * N + j] != ".":
                t = int(st[i * N + j]) - 1
                draw(i, j, t, True)
            else:
                cnt += 1

    dfs(cnt)
    print("".join(st))

最短路 188. 武士风度的牛

题目大意：农民 John 想交易他的一头被 Don 称为 The Knight 的牛。这头牛有特殊能力，可以按照象棋中马的走法跳跃。农场被表示为一个二维坐标图，其中包含了树、灌木、石头以及草的位置。The Knight 起始位置为 K，草的位置为 H。任务是确定 The Knight 要跳多少次才能到达草的位置。

实现思路：

首先解析输入，得到农场的列数和行数，以及地图信息，包括障碍物和目标位置（草的位置）。
使用广度优先搜索（BFS）算法来找到从起始位置到达目标位置的最短路径。
初始化一个队列，并将起始位置加入队列中。
在循环中，每次从队列中取出一个位置，并尝试向八个方向跳跃（象棋中马的所有可能走法），如果跳跃后的位置合法且没有障碍物且未被访问过，则将该位置加入队列，并标记为已访问。
当取出的位置为目标位置时，输出跳跃的次数，即最短路径的长度，然后退出循环。
如果队列为空仍未找到目标位置，则说明数据保证一定有解，不需要处理这种情况。

from collections import deque

dir = [(-2, 1), (-1, 2), (1, 2), (2, 1), (2, -1), (1, -2), (-1, -2), (-2, -1)]

c, r = map(int, input().split())
g = [[] for _ in range(r)]
vis = [[False]*(c+1) for _ in range(r+1)]
for i in range(r):
    g[i] = list(input())
    for j, ch in enumerate(g[i]):
        if ch=='H':
            end = (i, j)
        if ch=='K':
            start = (i, j)

q = deque()
q.append((*start, 0))

while q:
    x, y, d= q.popleft()

    if (x, y)==end:
        print(d)
        break
    
    for i in range(8):
        a, b = x + dir[i][0], y + dir[i][1]
        if 0<=a<r and 0<=b<c:
            if g[a][b]!='*' and not vis[a][b]:
                vis[a][b] = True
                q.append((a, b, d+1))

多源BFS

题目大意：给定一个 N 行 M 列的 01 矩阵 A，定义矩阵中每个位置与所有值为1的位置的曼哈顿距离。曼哈顿距离为该位置与所有值为1的位置行坐标之差的绝对值与列坐标之差的绝对值之和。

实现思路：

首先读入矩阵的行数和列数，以及矩阵本身。
使用BFS（广度优先搜索）来计算每个位置到所有值为1的位置的距离。
初始化一个队列，将所有值为1的位置入队，距离初始化为0。
对队列进行BFS遍历，每次取出队首元素，计算其周围四个方向的位置，若位置合法且为0且未被访问过，则更新距离并入队。
最终输出距离矩阵B。

import sys
from collections import deque
input = lambda:sys.stdin.readline().strip()
N = int(1e3+10)
g = [[] for _ in range(N)]
dis = [[-1]*N for _ in range(N)]

n, m = map(int, input().split())

for i in range(1, n+1):
    g[i] = [0] + list(input())
 
q = deque()   
for i in range(1, n+1):
    for j in range(1, m+1):
        if g[i][j] == '1':
           q.append((i, j, 0))
           dis[i][j] = 0
           
dx = [1, 0, -1, 0]
dy = [0, 1, 0, -1]

while q:
    x, y, d = q.popleft()
    for i in range(4):
        xx = x+dx[i]; yy = y+dy[i]
        if xx>0 and xx<=n and yy>0 and yy<=m:
            if g[xx][yy] == '0' and dis[xx][yy] == -1:
                dis[xx][yy] = d+1
                q.append((xx, yy, d+1))


for i in range(1, n+1):
    print(*dis[i][1:m+1])

双端队列BFS175. 电路维修

题目大意：有一个电路板，由 R 行 C 列的网格组成，每个格点都是电线的接点，每个格子包含一个可旋转的电子元件，电子元件连接一条对角线上的两个接点。达达希望通过旋转最少数量的元件，使电源与发动装置通过若干条短缆相连，但因为某些元件的方向不正确，导致电路板可能处于断路的状态。需要计算最少旋转的次数来使得电源和发动机之间连通。

实现思路：可以使用广度优先搜索（BFS）来解决此问题。首先，初始化一个二维数组 d 用于存储从起点到每个点的最短距离。然后，利用广度优先搜索的方式遍历电路板的每个格点，如果发现某个格点的状态需要改变（即当前格点的元件方向与所需方向不一致），则更新该格点的状态并将其加入到队列中。最后，返回终点的最短距离即可，如果无法到达终点，则输出 “NO SOLUTION”。

import sys
input = lambda:sys.stdin.readline().strip()
from collections import deque

dire = [(-1, -1), (-1, 1), (1, 1), (1, -1)]
mov = [(-1, -1), (-1, 0), (0, 0), (0, -1)]
ch = "\\/\\/"

def bfs():
    dq = deque()
    d = [[float('inf')]*(c+1) for _ in range(r+1)]
    d[0][0] = 0
    dq.append((0, 0))
    
    while dq:
        x, y = dq.popleft()
        for i in range(4):
            xx, yy = x + dire[i][0], y + dire[i][1]
            if 0<=xx<=r and 0<=yy<=c:
                j, k = x+mov[i][0], y + mov[i][1]
                w = 1 if g[j][k] != ch[i] else 0
                
                if d[xx][yy] > d[x][y] + w:
                    d[xx][yy] = d[x][y] + w
                    if w:
                        dq.append((xx, yy))
                    else:
                        dq.appendleft((xx, yy))
    return -1 if d[r][c] == float('inf') else d[r][c]

t = int(input())
for _ in range(t):
    r, c = map(int, input().split())
    g = [input() for _ in range(r)]
    
    res = bfs()
    print(res if res != -1 else "NO SOLUTION")

`A*` 179. 八数码

题目大意：在一个 3×3 的网格中，数字 1∼8 与一个 x 恰好不重不漏地分布在这个网格中。可以通过把 x 与其上、下、左、右四个方向之一的数字交换（如果存在）来改变网格的状态，目标是通过最少的移动次数，使得网格变为正确排列。

实现思路：使用 A* 算法来解决该问题。首先，定义一个启发函数用于估计当前状态到达目标状态的最小移动次数。然后，利用 A* 算法进行搜索，不断更新当前状态到达目标状态的最小移动次数，并记录每一步的移动操作。最后，输出得到的完整行动记录即可。如果不存在解决方案，则输出 “unsolvable”。

from heapq import heappush, heappop

d = [(-1, 0), (0, 1), (1, 0), (0, -1)]
op = "urdl"

def heuristic(state): # 启发式
    ans = 0
    for i, st in enumerate(state):
        if st=='x': continue
        t = int(st)-1
        ans += abs(t//3 - i//3) + abs(t%3 - i%3)
    return ans

def astar():
    dis, pre = dict(), dict()
    end = "12345678x"
    dis[start] = 0
    h = []
    heappush(h, (heuristic(start), start))
    
    
    while h:
        _, state = heappop(h)
        if state == end:
            break
        
        x, y = divmod(state.index('x'), 3)
        src = state
        
        for i in range(4):
            a, b = x+d[i][0], y+d[i][1]
            if 0<=a<3 and 0<=b<3:
                ls = list(state)
                ls[3*x+y], ls[3*a+b] = ls[3*a+b], ls[3*x+y]
                new_state = ''.join(ls)
                
                if new_state not in dis or dis[new_state] > dis[src] + 1:
                    dis[new_state] = dis[src] + 1
                    pre[new_state] = (op[i], src)
                    
                    heappush(h, (dis[new_state] + heuristic(new_state), new_state))
                    
    ans = ''
    while end != start:
        ans = pre[end][0] + ans
        end = pre[end][1]
    return ans


start = ''.join(input().split())
s = start.replace('x', '')

cnt = sum(s[i]>s[j] for i in range(8) for j in range(i, 8))

if cnt&1:
    print("unsolvable")
else:
    print(astar())

`IDA*` 排书

寻找估价函数，一定小于等于真实值，并越接近真实值

这道题目要求给定 n 本书，每本书编号为 1 到 n，初始状态下，书是任意排列的。每次操作可以抽取其中连续的一段，再把这段插入到其他某个位置。目标是将书按照 1 到 n 的顺序依次排列。要求计算最少需要多少次操作。

实现思路：

首先定义一个函数 f()，用来计算当前状态与目标状态之间的最小操作次数。这个函数通过遍历每对相邻书的编号，判断它们是否连续，如果不连续则需要进行一次操作。最后返回操作次数。
然后定义一个深度优先搜索函数 dfs(u)，其中 u 表示当前搜索的深度。在每次搜索中，我们需要判断当前深度加上到目标状态的最小操作次数是否超过已经得到的最小操作次数，如果超过则直接返回 False，否则继续搜索。
在 dfs 函数中，首先判断如果当前状态已经是目标状态，则直接返回 True。否则，我们遍历所有可能的操作，从中选择一种操作方式，然后递归调用 dfs 函数。
在主程序中，依次读入每组数据，然后进行深度优先搜索，直到得到结果或者搜索深度达到 5。最后根据得到的结果输出最小操作次数或者 “5 or more”。

def f():
    res = 0
    for i in range(n-1):
        if a[i] != a[i+1]-1:
            res += 1
    return (res+2)//3

def dfs(u):
    global a
    if u + f() > dep:
        return False
    
    if f()==0: 
        return True
        
    for leng in range(n, 0, -1):
        for l in range(n-leng+1):
            r = l+leng-1
            for k in range(l, r+1):
                bk = a[:]
                
                j = l
                for i in range(k+1, r+1):
                    a[j] = bk[i]
                    j+=1
                    
                for i in range(l, k+1):
                    a[j] = bk[i]
                    j+=1
                
                if dfs(u+1):
                    return True
                
                a = bk[:]
                


t = int(input())
while t:
    t-=1
    
    n = int(input())
    a = list(map(int, input().split()))

    dep = 0
    
    while dep<5 and not dfs(0):
        dep += 1
    
    if dep < 5:
        print(dep)
    else:
        print("5 or more")

算法笔记（三）——图论（Python实现）#

图论#

树的存储#

邻接矩阵#

邻接表#

树和图的存储#

树和图的遍历#

DFS#

BFS#

拓扑排序#

奖金#

LCA#

祖孙询问#

最短路#

朴素Dijkstra#

堆优化版Dijkstra#

另一种写法#

Bellman-Ford#

SPFA#

判断负环#

floyd#

Prim#

Kruskal#

染色法#

匈牙利算法#

DFS之连通性#

魔板#

单词接龙#

分成互质组#

迭代加深 加成序列#

双向DFS 送礼物#

37. 解数独 \166. 数独#

最短路 188. 武士风度的牛#

多源BFS#

双端队列BFS175. 电路维修#

A* 179. 八数码#

IDA* 排书#

算法笔记（三）——图论（Python实现）

图论

树的存储

邻接矩阵

邻接表

树和图的存储

树和图的遍历

DFS

BFS

拓扑排序

奖金

LCA

祖孙询问

最短路

朴素Dijkstra

堆优化版Dijkstra

另一种写法

Bellman-Ford

SPFA

判断负环

floyd

Prim

Kruskal

染色法

匈牙利算法

DFS之连通性

魔板

单词接龙

分成互质组

迭代加深加成序列

双向DFS 送礼物

37. 解数独 \166. 数独

最短路 188. 武士风度的牛

多源BFS

双端队列BFS175. 电路维修

`A*` 179. 八数码

`IDA*` 排书