LeetCode笔记
目标:2500分
HOT100
301. 删除无效的括号
题目大意:
给你一个由若干括号和字母组成的字符串 s ,删除最小数量的无效括号,使得输入的字符串有效。
返回所有可能的结果。答案可以按 任意顺序 返回。
回溯
实现思路:
-
统计无效括号数量:
- 首先遍历字符串s,统计左括号和右括号的数量l和r,其中l表示未匹配的左括号数量,r表示需要删除的右括号数量。
-
回溯算法:
- 编写回溯算法来尝试删除不同位置的括号,使得字符串有效。
- 回溯过程中需要注意以下情况:
- 已经匹配的括号数量ln和rn,以及当前位置i。
- 遍历字符串s的每个字符,当遇到重复的字符时跳过,以避免重复结果。
- 如果当前字符为左括号并且ln不为0,则递归调用删除当前左括号的情况,ln减一,否则继续。
- 如果当前字符为右括号并且rn不为0,则递归调用删除当前右括号的情况,rn减一,否则继续。
-
检查字符串有效性:
- 编写辅助函数
check来检查字符串是否有效,即左右括号数量是否匹配。
- 编写辅助函数
-
返回结果:
- 将所有有效的字符串结果添加到结果列表ret中,并返回。
class Solution:
def removeInvalidParentheses(self, s: str) -> List[str]:
l, r = 0, 0
ret = []
n = len(s)
for c in s:
if c=='(':
l+=1
elif c==')':
if l==0:
r+=1
else:
l-=1
def check(st):
cnt=0
for c in st:
if c=='(':
cnt+=1
elif c==')':
cnt-=1
if cnt<0:
return False
return (cnt==0)
def backtrace(st, start, ln, rn):
if ln==0 and rn==0 and check(st):
ret.append(st[:])
return
for i in range(start, len(st)):
if i>start and st[i]==st[i-1]:
continue
if ln+rn>n-1-i+1:
break
if ln and st[i]=='(':
backtrace(st[:i]+st[i+1:], i, ln-1, rn)
elif rn and st[i]==')':
backtrace(st[:i]+st[i+1:], i, ln, rn-1)
backtrace(s, 0, l, r)
return ret
广搜
这个实现使用了广度优先搜索(BFS)的思路来解决问题。
-
BFS搜索:
- 使用一个集合
cur来存储当前层的所有字符串,初始时将输入的字符串s加入集合cur中。 - 在每一轮循环中,遍历当前集合
cur中的所有字符串,如果其中有字符串是有效的,则将其加入结果列表ret中。 - 如果结果列表
ret不为空,则跳出循环,表示已经找到了所有有效的字符串。 - 如果结果列表
ret为空,则需要继续进行下一轮搜索,将当前集合cur中的每个字符串,通过删除一个括号的方式,生成所有可能的下一层字符串,加入到集合nxt中。 - 更新当前集合
cur为nxt,继续下一轮搜索。
- 使用一个集合
-
检查字符串有效性:
- 定义一个辅助函数
check,用于检查字符串是否有效。 - 遍历字符串中的每个字符,遇到左括号时增加计数器
cnt,遇到右括号时如果cnt为0则返回False(表示右括号没有匹配的左括号),否则减少cnt。 - 最终判断
cnt是否为0,如果为0表示字符串有效。
- 定义一个辅助函数
-
返回结果:
- 返回结果列表
ret,其中存储了所有有效的字符串。
- 返回结果列表
class Solution:
def removeInvalidParentheses(self, s: str) -> List[str]:
ret = []
def check(st):
cnt=0
for c in st:
if c=='(':
cnt+=1
elif c==')':
if cnt==0:
return False
cnt-=1
return cnt==0
cur = set([s])
while True:
for st in cur:
if check(st):
ret.append(st)
if len(ret):
break
nxt = set()
for st in cur:
for i in range(len(st)):
if i>0 and st[i]==st[i-1]:
continue
if st[i]=='(' or st[i]==')':
nxt.add(st[:i]+st[i+1:])
cur = nxt
return ret
297. 二叉树的序列化与反序列化
不止第一次遇到了。
-
题目大意:序列化是将一个数据结构或对象转换为连续的比特位的操作,从而可以存储在文件或内存中,并且通过网络传输到另一个计算机环境中。本题要求设计一个算法来实现二叉树的序列化和反序列化,即将二叉树转换为字符串并将字符串转换回原始的二叉树结构。
-
实现思路:
- 序列化:使用递归将二叉树转换为字符串,根节点值与左右子树序列化结果之间使用空格分隔,空节点用 ‘#’ 表示。
- 反序列化:使用递归将字符串转换为二叉树。首先定义一个辅助函数 DerWork(),用于递归构建二叉树。在该函数中,按照前序遍历的顺序,依次提取字符串中的节点值,并根据节点值构建二叉树节点。如果节点值为 ‘#’,表示空节点,返回 None。否则,创建节点并递归构建其左右子树。
- 在反序列化过程中,使用一个全局变量 self.s 来记录当前待处理的字符串,每次递归处理后,将字符串中已经处理过的部分剔除,继续处理剩余部分。
- 最终返回根节点即可。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Codec:
def serialize(self, root):
"""Encodes a tree to a single string.
:type root: TreeNode
:rtype: str
"""
if not root:
return '#'
return str(root.val)+' '+self.serialize(root.left)+' '+self.serialize(root.right)
def deserialize(self, data):
"""Decodes your encoded data to tree.
:type data: str
:rtype: TreeNode
"""
self.s = data
return self.DerWork()
def DerWork(self):
if len(self.s)==0:
return None
try:
idx = self.s.index(' ')
except:
idx = -1
node = self.s if idx==-1 else self.s[:idx]
self.s = '' if idx==-1 else self.s[idx+1:]
if node=='#':
return None
t = TreeNode(int(node))
t.left = self.DerWork()
t.right = self.DerWork()
return t
# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))
84. 柱状图中最大的矩形
-
题目大意:给定 n 个非负整数,表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1。求在该柱状图中,能够勾勒出的矩形的最大面积。
-
实现思路:
- 使用单调栈解决问题。创建两个数组 l 和 r,分别记录每个柱子向左和向右第一个比其高度小的柱子的索引位置。
- 初始化一个空栈 stk。
- 遍历柱子的高度列表 heights:
- 若栈不为空且当前柱子的高度小于栈顶柱子的高度,则将栈顶元素弹出,并更新栈顶元素对应的 r 值为当前柱子的索引。
- 若栈为空或者当前柱子的高度大于栈顶柱子的高度,则将当前柱子的索引入栈。
- 在更新 r 值的同时,若栈不为空,则更新当前柱子的 l 值为栈顶元素的索引。
- 遍历完成后,对于每个柱子 i,计算以该柱子为高度的矩形面积为 (r[i] - l[i] - 1) * heights[i],取最大值即为所求的最大矩形面积。
- 若柱状图为空,则返回 0。
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
n=len(heights)
l, r = [-1]*(n+5), [n]*(n+5)
stk = list()
for i in range(n):
while stk and heights[stk[-1]]>=heights[i]:
r[stk[-1]]=i
stk.pop()
if stk: l[i]=stk[-1]
stk.append(i)
return max( (r[i]-l[i]-1)*heights[i] for i in range(n) ) if n>0 else 0
85. 最大矩形
-
题目大意:给定一个仅包含 0 和 1、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
-
实现思路:
- 将问题转化为矩形最大面积问题。
- 定义变量 area 用于记录最大矩形的面积。
- 创建二维数组 left,用于记录每个位置 (i, j) 左侧连续 1 的个数。
- 遍历二维矩阵,初始化 left 数组:
- 若当前位置为 ‘1’,则 left[i][j] 等于 left[i][j-1] + 1,否则为 0。
- 遍历矩阵的每一列,对于每一列 j,使用单调栈来计算以当前列为底边的最大矩形的面积:
- 初始化一个空栈 stk。
- 定义两个数组 up 和 down,分别记录当前位置上方第一个小于等于其高度的位置和下方第一个小于等于其高度的位置。
- 遍历矩阵的每一行 i,进行以下操作:
- 当栈不为空且栈顶位置对应的 left 值大于等于当前位置的 left 值时,弹出栈顶位置,并更新 down 值。
- 如果栈为空,则当前位置的 up 值为 -1,否则为栈顶位置。
- 将当前行索引入栈。
- 在计算当前列的矩形面积时,height 为 down[i] - up[i] - 1,宽度为 left[i][j],计算当前列的最大面积并更新 area。
- 返回最大面积 area。
class Solution:
def maximalRectangle(self, matrix: List[List[str]]) -> int:
# 转化为矩形最大面积问题
n, m = len(matrix), len(matrix[0])
area = 0
left = [[0]*m for _ in range(n)]
for i in range(n):
for j in range(m):
if matrix[i][j]=='1':
left[i][j] += left[i][j-1]+1 if j else 1
for j in range(m):
stk = []
up, down = [-1]*n, [n]*n
for i in range(n): #行
while stk and left[ stk[-1] ][j]>=left[i][j]:
down[stk[-1]] = i
stk.pop()
up[i] = stk[-1] if stk else -1
stk.append(i)
for i in range(n):
height = down[i]-up[i]-1
area = max(area, height*left[i][j])
return area
76. 最小覆盖子串
-
题目大意:给定字符串 s 和字符串 t,返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “"。
-
注意:
-
对于 t 中重复字符,子字符串中该字符数量必须不少于 t 中该字符数量。
-
如果 s 中存在这样的子串,保证它是唯一的答案。
-
-
-
实现思路:
- 使用双指针滑动窗口解决问题。
- 初始化 need 字典,用于记录字符串 t 中每个字符的出现次数。
- 初始化 needCnt 为 t 的长度 m,表示还需要的字符数量。
- 初始化左指针 left 为 0,并初始化结果变量 res 为一个长度为 n 的区间,初始值为 (0, n)。
- 遍历字符串 t,统计每个字符的出现次数并存储在 need 字典中。
- 遍历字符串 s,使用右指针 right 遍历每个字符:
- 若当前字符在 t 中出现,则 needCnt 减 1。
- 更新 need 字典中当前字符的出现次数。
- 若 needCnt 为 0,表示当前窗口包含了 t 中所有字符,进入内部循环:
- 移动左指针 left,直到当前窗口不再满足条件(即 need 字典中某个字符的出现次数大于 0)。
- 更新结果变量 res。
- 恢复左指针 left 和 needCnt。
- 返回结果字符串,若结果区间超出 s 的范围,则返回空字符串。
class Solution:
def minWindow(self, s: str, t: str) -> str:
n, m = len(s), len(t)
need = defaultdict(int)
needCnt = m
left = 0
res = (0, n)
for ch in t:
need[ch]+=1
for right, ch in enumerate(s):
if need[ch]>0:
needCnt-=1
need[ch]-=1
if needCnt==0:
while need[s[left]]!=0:
need[s[left]]+=1
left+=1
if right-left < res[1]-res[0]:
res = (left, right)
need[s[left]]+=1
needCnt+=1
left+=1
return '' if res[1]>n-1 else s[res[0]:res[1]+1]
312. 戳气球
- 题意:给定n个数字
num[0~n-1],每次戳破一个气球可以获得nums[i-1]*nums[i]*nums[i+1]个硬币,最两旁默认为1,问最终获得的最大硬币数量。 - 思路:区间DP,逆向思维, 思考如何放气球能使硬币最大,
f[i][j]代表开区间i~j可以获得的最大硬币, 先枚举小区间,再枚举大区间,枚举区间内每个数字,状态转移有:f[i][j] = max(f[i][j], f[i][k]+f[k][j]+nums[i]*nums[k]*nums[j])。最终输出f[0][n+1]
class Solution:
def maxCoins(self, nums: List[int]) -> int:
n = len(nums)
nums = [1]+nums+[1]
f = [[0]*(n+5) for _ in range(n+5)]
# 开区间 (left, right) 区间内能获得的最大硬币
for l in range(2,n+2): # len:2~n+1
for i in range(n+1-l+1): # left:0~n+1-len
j=i+l # right = left + len
for k in range(i+1, j): # 开区间(i,j) 即[i+1, j-1]
f[i][j] = max(f[i][j], f[i][k]+f[k][j]+nums[i]*nums[k]*nums[j])
return f[0][n+1]
301. 删除无效的括号
-
题目大意:给定一个由字母和括号组成的字符串s,要求删除最小数量的括号,使得字符串成为有效的括号组合,并返回所有可能的结果。
-
实现思路:
-
首先定义一个辅助函数check(st),用于检查字符串st是否为有效的括号组合。遍历字符串中的每个字符,维护一个计数器cnt,遇到左括号增加计数,遇到右括号减少计数,若出现cnt为负数,或者遍历结束后cnt不为0,则说明括号不匹配,返回False,否则返回True。
-
初始化一个空列表ret,用于存储结果。
-
初始化一个集合cur,初始时将输入字符串s作为唯一元素加入其中。
-
使用while循环,直到找到符合条件的结果为止:
-
遍历集合cur中的每个字符串,检查其是否为有效括号组合,若是则将其加入结果列表ret。
-
若结果列表ret不为空,则说明已找到符合条件的结果,结束循环。
-
否则,初始化一个空集合nxt,用于存储下一轮迭代的候选字符串集合。
-
遍历集合cur中的每个字符串,对于每个字符串,尝试删除一个字符(括号),生成新的字符串,并将其加入nxt中。
-
更新cur为nxt,继续下一轮迭代。
-
-
返回结果列表ret。
-
class Solution:
def removeInvalidParentheses(self, s: str) -> List[str]:
ret = []
def check(st):
cnt=0
for c in st:
if c=='(':
cnt+=1
elif c==')':
if cnt==0:
return False
cnt-=1
return cnt==0
cur = set([s])
while True:
for st in cur:
if check(st):
ret.append(st)
if len(ret):
break
nxt = set()
for st in cur:
for i in range(len(st)):
if i>0 and st[i]==st[i-1]:
continue
if st[i]=='(' or st[i]==')':
nxt.add(st[:i]+st[i+1:])
cur = nxt
return ret
11. 盛最多水的容器
-
题目大意:给定一个长度为n的整数数组
height,数组中的每个元素代表一条垂直线的高度。找出其中的两条线,使得它们与x轴构成的容器可以容纳最多的水。 -
实现思路:使用双指针法。初始化左指针l指向数组的起始位置,右指针r指向数组的末尾位置。设置变量
ret用于记录当前最大容量,初始化为0。在每一轮循环中,计算当前容器的容量,即min(height[l], height[r])乘以r和l之间的距离,更新ret。然后根据指针所指向的高度的大小,移动指针,如果height[l]<height[r],则移动左指针l向右一步,否则移动右指针r向左一步。直到左右指针相遇,循环结束,返回ret即可。- 正确性证明: 对于左右端点 $ l, r$, 两点之间的距离为$len = r-l+1-1$(因为两个点之间算一段,所以长度要减一),$ ret = (r-l)*min(height[l], height[r])$,假设 $height[l]<height[r]$, 对于左端点,其作为柱子能容纳的最多的水的数量已经为最大值,任意的 $l<x<r$ 作为右端点一定比$r$做端点更差,所以可以排除左端点$l$,计算下一点即$l+1$。从左右端点开始,对于每次排除的点,已经找到这个端点可能的最大值, 所以可以保证结果的正确性。
class Solution:
def maxArea(self, height: List[int]) -> int:
l, r = 0, len(height)-1
ret = 0
while l<r:
ret = max( ret, (r-l)*min(height[l], height[r]) )
if height[l]<height[r]:
l+=1
elif height[l]>height[r]:
r-=1
else:
l+=1
r-=1
return ret
647. 回文子串
题目大意:给定一个字符串s,统计并返回该字符串中回文子串的数目。回文字符串是指正着读和倒过来读一样的字符串。子字符串是字符串中的由连续字符组成的一个序列。即使是由相同字符组成的不同开始位置或结束位置的子串,也会被视作不同的子串。
实现思路:遍历字符串s的所有可能的中心位置,对于每个中心位置,向两边扩展,判断是否是回文串。在扩展的过程中,每当发现一个回文子串,就将计数器加1。最终返回计数器的值即可。
class Solution:
def countSubstrings(self, s: str) -> int:
n = len(s)
ans = 0
for i in range(2*n - 1):
l, r = i//2, i//2 + (i&1)
while l>=0 and r<n and s[l]==s[r]:
l-=1; r+=1
ans+=1
return ans
93. 复原 IP 地址
题目大意:给定一个只包含数字的字符串s,表示一个IP地址,要求返回所有可能的有效IP地址,即每个IP地址由四个整数组成(每个整数位于0到255之间,且不能含有前导0),整数之间用’.‘分隔。不能重新排序或删除s中的任何数字,可以按任何顺序返回答案。
实现思路:使用深度优先搜索(DFS)算法,递归地搜索所有可能的IP地址组合。在搜索过程中,首先确定每个整数的范围,然后遍历可能的数字组合,逐步构建IP地址。递归的终止条件是已经找到了四个整数并且已经遍历完了整个字符串s。
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
n = len(s)
res, addr = [], ['0']*4
def dfs(i, start):
if i==4 or start==n:
if i==4 and start==n:
res.append('.'.join(addr))
return
if s[start]=='0':
addr[i] = '0'
dfs(i+1, start+1)
return
num = 0
for end in range(start, n):
num = num*10 + int(s[end])
if num in range(256):
addr[i] = str(num)
dfs(i+1, end+1)
dfs(0, 0)
return res
538. 把二叉搜索树转换为累加树
题目大意:给定一个二叉搜索树的根节点,需要将其转换为累加树,即每个节点的新值等于原树中大于或等于该节点值的节点值之和。
class Solution:
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
s = 0
def dfs(r):
nonlocal s
if not r:
return 0
dfs(r.right)
s += r.val
r.val = s
dfs(r.left)
dfs(root)
return root
实现思路:**(Morris 遍历)**从根节点开始,采用反向中序遍历(右-根-左)的方式进行遍历。利用一个变量 s 记录累加和,初始值为 0。对于每个节点,首先判断其是否存在右子节点,如果不存在,则将其值加上累加和并更新累加和,然后将当前节点指向其左子节点;如果存在右子节点,则找到其中序遍历的后继节点,即右子树中最左边的节点。如果后继节点的左子节点为空,说明还未处理过该节点,则将后继节点的左子节点指向当前节点,并将当前节点指向其右子节点;如果后继节点的左子节点为当前节点,则说明已经处理过该节点,则将后继节点的左子节点置为空,将当前节点的值加上累加和并更新累加和,并将当前节点指向其左子节点。最后返回根节点。
class Solution:
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
def getSucc(node):
succ = node.right
while succ.left and succ.left!=node:
succ = succ.left
return succ
newRoot = root
s = 0
while root:
if not root.right:
s += root.val
root.val = s
root = root.left
else:
succ = getSucc(root)
if not succ.left:
succ.left = root
root = root.right
else:
succ.left = None
s += root.val
root.val = s
root = root.left
return newRoot
15. 三数之和
题目大意:给定一个整数数组 nums,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k,同时还满足 nums[i] + nums[j] + nums[k] == 0。返回所有满足条件的不重复的三元组。
实现思路:首先对数组 nums 进行排序。然后遍历数组,对于每个元素 nums[i],设定两个指针 l 和 r 分别指向 i+1 和数组末尾。在 l 和 r 之间寻找和为 0 的两个数。具体地,如果当前元素与前一个元素相同,跳过;如果当前元素与 l+1 处的元素相同,跳过;在 l 和 r 之间利用双指针的方式找到满足条件的两个数,如果找到了满足条件的三元组,则添加到结果中。最后返回结果列表 res。
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
nums.sort()
res = []
for i in range(n):
l = i
r = n-1
if i and nums[i]==nums[i-1]:
continue
for m in range(l+1, n):
if m>l+1 and nums[m]==nums[m-1]:
continue
while r>m and nums[r]+nums[m]+nums[l]>0:
r-=1
if m==r: break
if nums[r]+nums[m]+nums[l]==0:
res.append([nums[l], nums[m], nums[r]])
return res
实现思路:首先,利用 Counter 函数统计每个数出现的次数,并检查是否有 0 出现至少三次,如果是则将 [0, 0, 0] 添加到结果中。然后,对不重复的数进行排序。遍历排序后的数,对于每个数 num,如果 num 不等于 0 且 num 出现次数大于 1 且 -num*2 也在 Counter 中,则将 [num, num, -num*2] 添加到结果中。然后,在负数部分,利用双指针的方式寻找满足条件的两个数。最后返回结果列表 res。
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
res = []
c = Counter(nums)
if 0 in c and c[0] >= 3:
res.append([0,0,0])
no_repeat_nums = sorted(c.keys())
for i,num in enumerate(no_repeat_nums):
if num != 0 and c[num] > 1 and -num*2 in c:
res.append([num,num,-num*2])
if num < 0:
for num3 in no_repeat_nums[ bisect_left(no_repeat_nums,((-num+1)/2)) : bisect_right(no_repeat_nums,-num*2-1) ]:
num2 = -num-num3
if num2 in c:
res.append([num,num2,num3])
return res
494. 目标和
题目大意:给定一个非负整数数组 nums 和一个目标整数 target,通过给数组中的每个整数前添加 ‘+’ 或 ‘-’,然后串联起来构造表达式,返回可以构造的表达式数目,使其运算结果等于目标数。
记忆化搜索
实现思路:这个问题可以转化为一个背包问题。我们可以将问题转化为在数组中选取一些数,使得它们的和等于 target。定义一个递归函数 dfs(i, s),表示在数组 nums 中考虑第 i 个数,使得目前的和为 s 的表达式数目。递归的终止条件是遍历完所有数,如果 s 等于 0,表示找到了一种构造方式,返回 1,否则返回 0。递归过程中,如果 s 小于当前数 nums[i],说明无法选取当前数,直接跳过;否则,递归考虑选取当前数和不选取当前数两种情况。利用缓存装饰器 @cache 可以将重复计算的结果进行缓存,提高计算效率。最后返回 dfs(0, target) 即可得到结果。
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
target += sum(nums)
if target<0 or target&1:
return 0
target//=2
@cache
def dfs(i, s):
if i==len(nums):
return 1 if s==0 else 0
if s<nums[i]:
return dfs(i+1, s)
else:
return dfs(i+1, s) + dfs(i+1, s-nums[i])
return dfs(0, target)
动态规划
实现思路:这里采用动态规划来解决。首先将目标数 target 加上数组 nums 的总和,如果总和为负数或者是奇数,则无法通过调整符号得到目标数,直接返回 0。否则,将目标数除以 2,然后定义一个二维数组 f,其中 f[i][j] 表示在考虑前 i 个数时,构造和为 j 的表达式的数目。初始化 f[0][0] = 1。然后,遍历数组 nums,并且更新 f[i][j]。当 j 小于当前数 nums[i-1] 时,表示无法选取当前数,则 f[i][j] 等于上一个状态的值;当 j 大于等于当前数 nums[i-1] 时,可以选择加上或减去当前数,则 f[i][j] 等于上一个状态加上不选取当前数的值以及上一个状态加上选取当前数的值。最后返回 f[n][target],其中 n 是数组 nums 的长度。
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
target+=sum(nums)
if target<0 or target%2:
return 0
target//=2
n = len(nums)
f = [[0]*(target+1) for _ in range(n+1)]
f[0][0] = 1
for i in range(1, n+1):
for j in range(target+1):
if j<nums[i-1]:
f[i][j] = f[i-1][j]
else:
f[i][j] = f[i-1][j] + f[i-1][j-nums[i-1]]
return f[n][target]
581. 最短无序连续子数组
题目大意:给定一个整数数组 nums,找出一个连续子数组,使得对该子数组进行升序排序后,整个数组都变为升序排序。要求找出符合题意的最短子数组,并输出其长度。
实现思路:使用两个指针left和right,初始化为-1,遍历数组nums。首先,从左到右找到第一个无序的元素,即当前元素小于前面已遍历过的最大元素,此时更新right指针为当前位置i;然后,从右到左找到第一个无序的元素,即当前元素大于后面已遍历过的最小元素,此时更新left指针为当前位置n-i-1。最终返回right-left+1即为最短无序连续子数组的长度。
class Solution:
def findUnsortedSubarray(self, nums: List[int]) -> int:
n = len(nums)
ma, right = -inf, -1
mi, left = inf, -1
for i in range(n):
if ma>nums[i]:
right = i
else:
ma = nums[i]
if mi<nums[n-i-1]:
left = n-i-1
else:
mi = nums[n-i-1]
return 0 if right==-1 else right-left+1
416. 分割等和子集
题目大意:给定一个非空数组 nums,数组中只包含正整数。要求判断是否能将该数组分割成两个子集,使得这两个子集的元素和相等。
实现思路:
- 首先计算数组 nums 的总和 s。
- 如果总和 s 为奇数,那么无法分割成两个和相等的子集,直接返回 False。
- 如果数组中的最大值大于总和的一半,则无法分割成两个和相等的子集,直接返回 False。
- 初始化一个大小为总和一半加一的布尔数组 f,f[i] 表示是否存在子集的和为 i。
- 将 f[0] 初始化为 True,表示子集的和为 0。
- 遍历数组 nums,对于每个正整数 num,从总和一半开始向前遍历,更新数组 f,如果 f[j-num] 为 True,则说明存在一个子集的和为 j-num,加上当前的 num 后,和为 j,因此 f[j] 也为 True。
- 最终返回 f[s//2],表示是否存在一个子集的和为总和一半,即是否能分割成两个和相等的子集。
class Solution:
def canPartition(self, nums: List[int]) -> bool:
s = sum(nums)
if s&1: return False
ma = max(nums)
t = s//2
if ma>t: return False
n = len(nums)
f = [False]*(t+1)
f[0] = True
for i, num in enumerate(nums):
for j in range(t, num-1, -1):
f[j] |= f[j-num]
return f[t]
394. 字符串解码
题目大意:给定一个经过编码的字符串,其中编码规则为k[encoded_string],表示encoded_string中的内容重复k次。要求解码该字符串。
实现思路:使用递归来解码字符串。遍历输入字符串,根据不同情况进行处理:
- 若遇到数字,则累加数字直至遇到非数字字符。
- 若遇到字母,则直接加入当前解码的字符串中。
- 若遇到左括号’[’,则递归调用解码函数,处理括号内的内容,直至遇到右括号’]’。将括号内的解码结果乘以前面累积的数字,并加入当前解码的字符串中。
- 若遇到右括号’]’,则返回当前解码的字符串和当前索引。
- 返回最终解码结果。
class Solution:
def decodeString(self, s: str) -> str:
def decode(i, n):
cur = ""; num = 0
while i<len(s):
if s[i].isdigit():
num = num*10 + int(s[i])
elif s[i].isalpha():
cur += s[i]
elif s[i] == '[':
ns, ni = decode(i+1, num) # next str, next index
cur += ns; i = ni
num = 0
elif s[i]==']':
return cur*n, i
i += 1
return cur*n, i
res, _ = decode(0, 1)
return res
72. 编辑距离
题目大意: 给定两个单词 word1 和 word2,求通过插入、删除或替换字符,将 word1 转换成 word2 所需的最少操作数。
记忆化搜索
这段代码使用了递归的方式求解,其中 dfs 函数表示将 s 的前 i 个字符转换为 t 的前 j 个字符所需的最少操作数。递归的基本情况是当 i 小于 0 时,表示 s 已经遍历完,需要插入 t 的前 j+1 个字符;当 j 小于 0 时,表示 t 已经遍历完,需要删除 s 的前 i+1 个字符;当 s[i] 等于 t[j] 时,不需要额外操作,直接递归处理 i-1 和 j-1;当 s[i] 不等于 t[j] 时,可以选择插入、删除或替换操作,选择操作数最小的方案。递归的过程中利用了缓存装饰器 @cache 来提高效率。
class Solution:
def minDistance(self, s: str, t: str) -> int:
n, m = len(s), len(t)
@cache
def dfs(i, j):
if i<0: return j+1
if j<0: return i+1
if s[i]==t[j]: return dfs(i-1, j-1)
return min(dfs(i-1, j), dfs(i, j-1), dfs(i-1, j-1)) + 1
return dfs(n-1, m-1)
递推
实现思路:
可以使用动态规划来解决这个问题。定义一个二维数组 f,其中 f[i][j] 表示将 word1 的前 i 个字符转换为 word2 的前 j 个字符所需的最少操作数。初始时,f[i][0] 表示将 word1 的前 i 个字符全部删除,需要的操作数为 i,而 f[0][j] 表示将 word2 的前 j 个字符全部插入到 word1 中,需要的操作数为 j。
然后,根据动态规划的状态转移方程,逐步计算 f[i][j] 的值。若 word1[i] 等于 word2[j],则 f[i][j] 等于 f[i-1][j-1],即不需要额外操作;若不相等,则可以考虑插入、删除或替换操作,选择操作数最小的方案。最终,返回 f[n][m],其中 n 和 m 分别为 word1 和 word2 的长度。
class Solution:
def minDistance(self, s: str, t: str) -> int:
n, m = len(s), len(t)
f = [[0]*(m+1) for _ in range(n+1)]
f[0] = list(range(m+1)) # f[0][j] = j
for i in range(n):
f[i+1][0] = i+1
for j in range(m):
if s[i]==t[j]:
f[i+1][j+1] = f[i][j]
else:
f[i+1][j+1] = min(f[i][j+1], f[i+1][j], f[i][j]) + 1
return f[n][m]
96. 不同的二叉搜索树
class Solution:
def numTrees(self, n: int) -> int:
f = [0]*(n+1)
f[0] = 1; f[1] = 1
for i in range(2, n+1):
for j in range(1, i+1):
f[i] += f[i-j]*f[j-1]
return f[n]
160. 相交链表
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
l1, l2 = headA, headB
while l1 != l2:
l1 = headB if not l1 else l1.next
l2 = headA if not l2 else l2.next
return l1
31. 下一个排列
题目大意:给定一个整数数组,要求找出这个数组的下一个排列,即比当前排列大的下一个排列,如果不存在则返回字典序最小的排列。
实现思路:要找到下一个排列,可以遵循以下步骤:
- 从数组末尾开始,找到第一个相邻的两个数,满足 nums[i] < nums[i+1]。
- 如果找到了这样的一对数,说明当前排列还不是最大的排列,可以进行下一步操作。
- 在从右往左找到的第一个位置记为 i,再从数组末尾开始,找到第一个大于 nums[i] 的数,记为 j。
- 交换 nums[i] 和 nums[j]。
- 将从 i+1 位置开始到数组末尾的数逆序排列,以得到字典序最小的排列。
- 如果步骤1中没有找到相邻的两个数,则说明当前排列已经是最大的排列,直接将整个数组逆序排列即可。
class Solution:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
n = len(nums)
i = n-2
while i>=0 and nums[i] >= nums[i+1]:
i-=1
if i>=0:
j = n-1
while j>=i and nums[j] <= nums[i]:
j-=1
nums[i], nums[j] = nums[j], nums[i]
nums[i+1:] = reversed(nums[i+1:])
33. 搜索旋转排序数组
题目大意:
给定一个按升序排列的整数数组 nums,数组中的值互不相同。该数组经过未知的某个下标旋转,即原本排在数组开头的一部分元素被移动到数组末尾。给定一个目标值 target,如果该目标值存在于旋转后的数组中,则返回其下标,否则返回 -1。要求设计一个时间复杂度为 O(log n) 的算法解决此问题。
实现思路:
- 使用二分查找算法来解决此问题,以满足 O(log n) 的时间复杂度要求。
- 初始化左右指针
l和r分别指向数组的首尾元素。 - 在循环中,计算中间位置
mid,判断nums[mid]是否等于目标值target,若是则直接返回mid。 - 若
nums[0] <= nums[mid],说明左半段是有序的,此时判断目标值是否在左半段范围内,若是则将右指针移到mid-1,否则将左指针移到mid+1。 - 若
nums[0] > nums[mid],说明右半段是有序的,此时判断目标值是否在右半段范围内,若是则将左指针移到mid+1,否则将右指针移到mid-1。 - 若循环结束仍未找到目标值,则返回 -1。
class Solution:
def search(self, nums: List[int], target: int) -> int:
if not nums: return -1
n = len(nums)
l, r = 0, n-1
while l<=r:
mid = l+r>>1
if nums[mid]==target:
return mid
if nums[0]<=nums[mid]:
if nums[0] <= target < nums[mid]:
r = mid-1
else:
l = mid+1
else:
if nums[mid] < target <= nums[n-1]:
l = mid+1
else:
r = mid-1
return -1
19. 删除链表的倒数第 N 个结点
题目大意:给定一个链表,要求删除倒数第n个节点,并返回链表的头结点。
实现思路:使用双指针,首先让第一个指针从头节点开始向后移动n步,然后同时移动第一个指针和第二个指针,直到第一个指针到达链表末尾。这样第二个指针所指的位置就是倒数第n个节点的前一个节点,然后进行删除操作即可。需要注意的是要考虑边界情况,比如链表长度为1,删除头节点等情况。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
if not head.next:
return None
p1 = head
n-=1
while n:
p1 = p1.next
n-=1
pre = p2 = head
while p1.next:
p1 = p1.next
pre = p2
p2 = p2.next
if p2==head:
head = head.next
else:
pre.next = pre.next.next
return head
148. 排序链表
题目大意:给定一个链表的头结点head,要求将链表按升序排列,并返回排序后的链表。
实现思路:
- 使用归并排序的思想对链表进行排序。
- 编写递归函数sortFun(head, tail),其中head表示当前待排序的子链表的头结点,tail表示当前待排序的子链表的尾结点的下一个结点(即尾结点的后继结点)。
- 在sortFun函数中,使用快慢指针找到当前待排序子链表的中间结点mid,并将链表分为两部分,左边部分由head到mid-1,右边部分由mid到tail-1。
- 递归调用sortFun函数对左右两部分进行排序,直至排序完成。
- 编写merge函数,将已经排好序的左右两部分链表进行合并,合并过程中按照结点的值大小进行比较,将较小的结点连接到结果链表中。
- 返回合并后的链表。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
def sortFun(head, tail):
if not head:
return head
if head.next == tail:
head.next = None
return head
slow = fast = head
while fast != tail:
fast = fast.next
slow = slow.next
if fast != tail:
fast = fast.next
mid = slow
return merge(sortFun(head, mid), sortFun(mid, tail))
def merge(h1, h2):
dummy = ListNode(-1)
cur = dummy
while h1 and h2:
if h1.val<=h2.val:
cur.next = h1
h1 = h1.next
else:
cur.next = h2
h2 = h2.next
cur = cur.next
if h1:
cur.next = h1
if h2:
cur.next = h2
return dummy.next
return sortFun(head, None)
581. 最短无序连续子数组
题目大意:给定一个整数数组nums,找出一个连续子数组,使得对该子数组进行升序排序后,整个数组都变为升序排序。要求找出符合条件的最短子数组,并输出其长度。
实现思路:
- 首先初始化最大值mx为负无穷,最小值mn为正无穷,以及最短子数组的左右边界left和right分别为-1。
- 遍历数组nums,从左向右寻找右边界right,如果当前元素小于前面的最大值mx,则更新right为当前索引;否则更新最大值mx为当前元素。
- 同时,从右向左寻找左边界left,如果当前元素大于后面的最小值mn,则更新left为当前索引;否则更新最小值mn为当前元素。
- 最后返回右边界和左边界的差加1,即为最短子数组的长度。如果左边界仍为初始值-1,则返回0表示整个数组已经有序。
class Solution:
def findUnsortedSubarray(self, nums: List[int]) -> int:
n = len(nums)
mx, right = -inf, -1
mn, left = inf, -1
for i in range(n):
if mx>nums[i]:
right = i
else:
mx = nums[i]
if mn<nums[n-1-i]:
left = n-1-i
else:
mn = nums[n-1-i]
return 0 if left==-1 else right-left+1
线段树
729. 我的日程安排表 I
- 题目大意:这个题目是关于设计一个日程安排类
MyCalendar,它能够存储日程,并判断是否会有重复预订。日程以半开区间[start, end)表示,当两个日程时间有交叠时就会产生重复预订。
实现思路:
-
使用线段树:
- 我们可以使用线段树来表示时间段的预订情况。每个节点代表一个时间段,节点值表示这个时间段是否被预订。
- 对于每个节点,我们维护两个集合,
self.tree表示已经预订的节点,self.lazy表示已经被标记为预订但尚未被更新的节点。
-
查询功能:
- 当需要查询某个时间段是否被预订时,我们可以在线段树上进行查询。如果查询到某个节点被标记为已预订(包括被标记为预订但尚未更新的节点),则返回预订;否则返回未预订。
-
更新功能:
- 当要预订某个时间段时,我们在线段树上进行更新操作。首先从根节点开始,递归地向下更新,将该时间段的节点标记为已预订,并将经过的节点加入
self.tree中。 - 同时,如果该节点的两个子节点都被标记为已预订,则将该节点也标记为已预订,同时加入
self.lazy中,表示其下的所有节点都已经被预订但尚未更新。
- 当要预订某个时间段时,我们在线段树上进行更新操作。首先从根节点开始,递归地向下更新,将该时间段的节点标记为已预订,并将经过的节点加入
-
book 方法:
- 在
book方法中,首先判断要预订的时间段是否已经被预订,如果是,则返回False;否则,调用update方法进行更新,并返回True。
- 在
class MyCalendar:
def __init__(self):
self.tree = set()
self.lazy = set()
def query(self, start: int, end: int, l: int, r: int, idx: int) -> bool:
if r < start or end < l:
return False
if idx in self.lazy: # 如果该区间已被预订,则直接返回
return True
if start <= l and r <= end:
return idx in self.tree
mid = (l + r) // 2
return self.query(start, end, l, mid, 2 * idx) or \
self.query(start, end, mid + 1, r, 2 * idx + 1)
def update(self, start, end, l, r, idx):
if start>r or end<l:
return False
if start<=l and r<=end:
self.tree.add(idx)
self.lazy.add(idx)
else:
mid = (l+r)>>1
self.update(start, end, l, mid, idx*2)
self.update(start, end, mid+1, r, idx*2+1)
self.tree.add(idx)
if 2*idx in self.lazy and 2*idx+1 in self.lazy:
self.lazy.add(idx)
def book(self, start: int, end: int) -> bool:
if self.query(start, end-1, 0, 10**9, 1):
return False
self.update(start, end-1, 0, 10**9, 1)
return True
2286. 以组为单位订音乐会的门票
题目大意: 设计一个买票系统,针对音乐会的座位安排。音乐会总共有n排座位,每排有m个座椅。系统需要处理两种情况:
gather(k, maxRow): 返回长度为2的数组,表示k个成员中第一个座位的排数和座位编号,这k位成员必须坐在同一排座位,且座位连续。如果无法安排座位,返回空数组。scatter(k, maxRow): 如果组里所有k个成员不一定要坐在一起的前提下,都能在第0排到第maxRow排之间找到座位,返回true;否则返回false。这种情况下,每个成员都优先找排数最小,然后是座位编号最小的座位。
实现思路:
- 对于
gather(k, maxRow),可以利用线段树来实现。- 线段树节点维护最小值和总和,用于查找最小值以及查询总和。
- 使用二分查找确定符合条件的最小排数,并更新座位信息。
- 对于
scatter(k, maxRow),同样使用线段树来维护座位信息。- 遍历排数,根据当前排的剩余座位数量和需求
k进行判断。 - 若当前排剩余座位数足够,安排
k个座位并返回true;若不足够,继续向下一排尝试。
- 遍历排数,根据当前排的剩余座位数量和需求
class BookMyShow:
def __init__(self, n: int, m: int):
self.n, self.m = n, m
N = 1 << n.bit_length() + 1
self.mn = [0] * N # min
self.sm = [0] * N # sum
def modify(self, u, l, r, x, v):
if l == r:
self.mn[u] += v
self.sm[u] += v
else:
mid = l + r >> 1
if x <= mid:
self.modify(u << 1, l, mid, x, v)
else:
self.modify(u << 1 | 1, mid + 1, r, x, v)
self.mn[u] = min(self.mn[u << 1], self.mn[u << 1 | 1])
self.sm[u] = self.sm[u << 1] + self.sm[u << 1 | 1]
def query(self, u, l, r, ql, qr):
if l >= ql and r <= qr:
return self.sm[u]
mid = l + r >> 1
res = 0
if ql <= mid:
res = self.query(u << 1, l, mid, ql, qr)
if qr > mid:
res += self.query(u << 1 | 1, mid + 1, r, ql, qr)
return res
def index(self, u, l, r, qr, v):
if self.mn[u] > v:
return 0
if l == r:
return l
mid = l + r >> 1
if self.mn[u << 1] <= v:
return self.index(u << 1, l, mid, qr, v)
if qr > mid:
return self.index(u << 1 | 1, mid + 1, r, qr, v)
return 0
def gather(self, k: int, maxRow: int) -> List[int]:
i = self.index(1, 1, self.n, maxRow + 1, self.m - k)
if i == 0:
return []
col = self.query(1, 1, self.n, i, i)
self.modify(1, 1, self.n, i, k)
return [i - 1, col]
def scatter(self, k: int, maxRow: int) -> bool:
if self.m * (maxRow + 1) - self.query(1, 1, self.n, 1, maxRow + 1) < k:
return False
i = self.index(1, 1, self.n, maxRow + 1, self.m - 1)
while True:
rest = self.m - self.query(1, 1, self.n, i, i)
if k <= rest:
self.modify(1, 1, self.n, i, k)
return True
self.modify(1, 1, self.n, i, rest)
k -= rest
i += 1
其他题目
3031. 将单词恢复初始状态所需的最短时间 II Z函数
题目大意: 给定一个字符串 word 和一个整数 k,每秒需要执行两种操作:移除字符串 word 的前 k 个字符,并在字符串末尾添加 k 个任意字符。要求返回将 word 恢复到初始状态所需的最短时间。
实现思路: 首先,我们可以利用 Z 函数(Z algorithm)来找到字符串的最长前缀后缀匹配长度。然后,我们可以利用 Z 函数的性质,将字符串分割成不同的前缀子串,找到满足条件的最小时间。
具体步骤如下:
- 初始化一个数组 z,用于存储字符串 s 的 Z 函数值。
- 使用双指针 l 和 r 来维护当前匹配的子串。
- 遍历字符串 s,计算 z[i] 的值,即以第 i 个字符为起始的最长前缀后缀匹配长度。
- 在每次遍历中,更新 l 和 r 的值,保持当前匹配的子串范围。
- 如果当前位置 i 能够满足条件:即 i 是 k 的倍数且 z[i] 等于剩余字符串的长度(n - i),则返回 i 除以 k。
- 若遍历完字符串后仍未找到满足条件的位置,则返回 (n - 1) 除以 k 再加 1,表示需要把剩余的字符串都移除并添加到末尾。
class Solution:
def minimumTimeToInitialState(self, s: str, k: int) -> int:
n = len(s)
z = [0] * n
l, r = 0, 0
for i in range(1, n):
if i <= r and z[i - l] < r - i + 1:
z[i] = z[i - l]
else:
z[i] = max(0, r - i + 1)
while i + z[i] < n and s[z[i]] == s[i + z[i]]:
z[i] += 1
if i + z[i] - 1 > r:
l = i
r = i + z[i] - 1
if i%k==0 and z[i] == n-i:
return i//k
return (n-1)//k+1
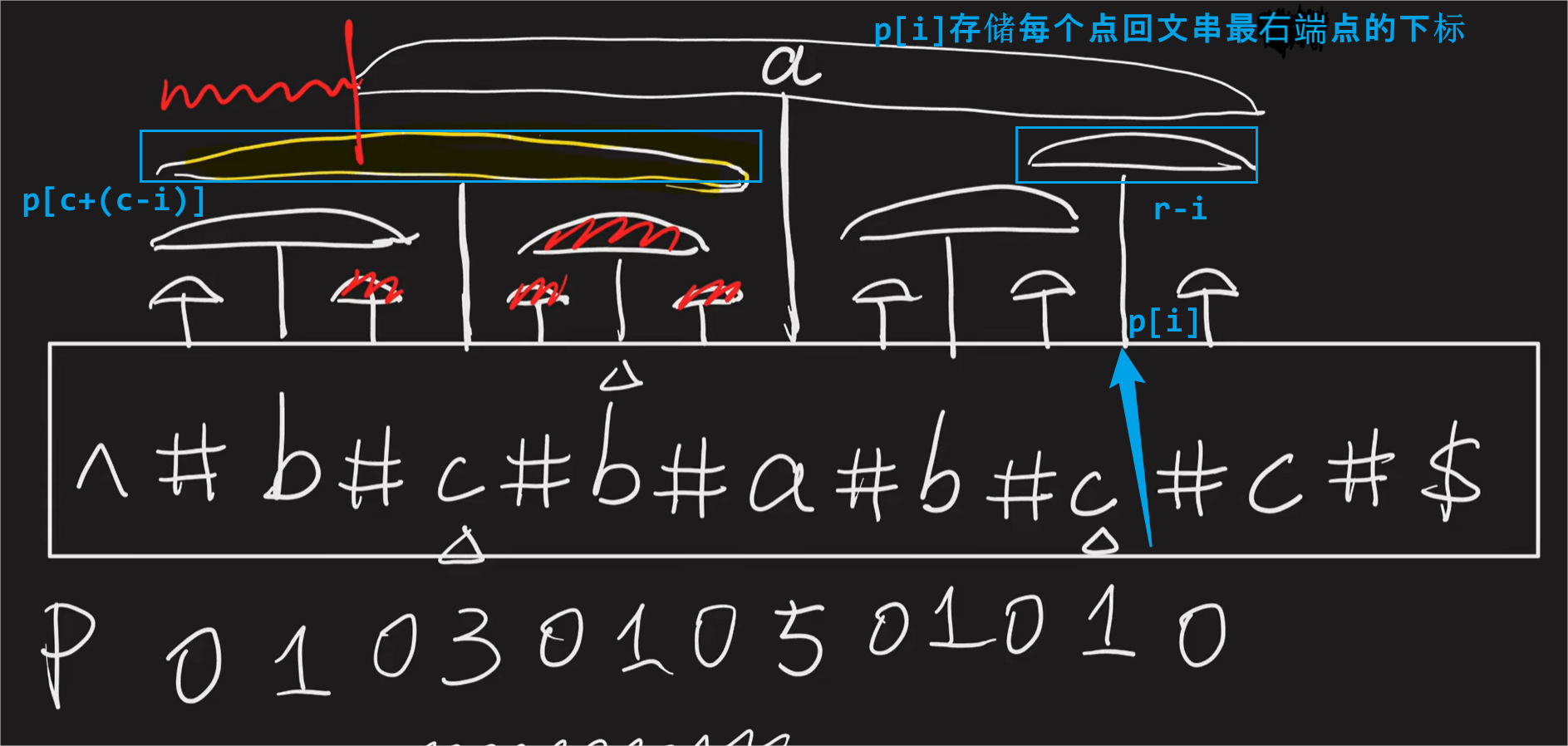
5. 最长回文子串马拉车算法
- 题意:求字符串内的最大回文串长度
- 思路:马拉车算法,由当前已知的最大回文串长度,我们可以由已知的回文串长度,推出其覆盖的点的最大回文串长度。如下图,p[i]位置的回文串长度可以由最长的回文串(以
a为中心)得出,因为回文串两边是对称的,所以p[i] = p[c + c-i], 但是对于覆盖不到的部分,需要取下限r-i。
class Solution:
# 推荐教学视频 :https://www.bilibili.com/video/BV1Sx4y1k7jG/?spm_id_from=333.337.search-card.all.click&vd_source=a4a2b56f746715b34521bfb853094cf4
def longestPalindrome(self, s: str) -> str:
s = '#' + '#'.join(list(s)) + '#'
n = len(s)
p = [0]*n #每个点的 最长回文字串 能到的 右侧位置
c, r = 0, 0 # 右边能到达最远的蘑菇的位置 和 其最右边能达到的位置
for i in range(n):
if i<=r:
p[i] = min(r-i, p[c + c-i]) # 由已知条件得到当前位置能达到的最大右侧距离( 需要取min(镜像位置的值, 当前最大蘑菇能覆盖到的最大值) )
while i+p[i]+1 < n and s[i-p[i]-1] == s[i+p[i]+1]:
p[i]+=1
if p[i]+i > r:
r = p[i] + i
c = i
ma = max(p)
idx = p.index(ma)
return s[idx-ma+1:idx+ma+1:2]